Explaining machine learning models with SHAP and SAGE

---

---

Machine learning (ML) models are complicated, particularly expressive models like decision forests and neural networks. No interpretability tool provides a perfect understanding of the model or a solution for all our needs, so we need different tools to understand our models in different ways. In this post we'll discuss SHAP [1] and SAGE [2], two game theoretic methods based on the Shapley value.

Each method answers a specific type of question:

• SHAP answers the question how much does each feature contribute to this individual prediction?
• SAGE answers the question how much does the model depend on each feature overall?

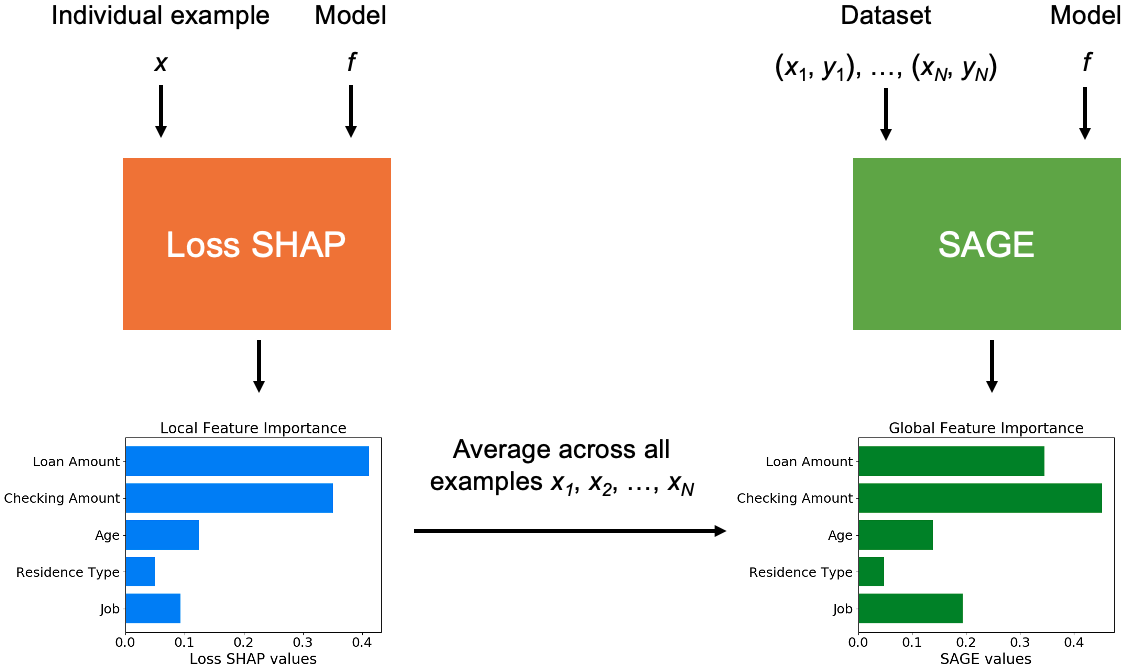
SHAP is a method for explaining individual predictions (local interpretability), whereas SAGE is a method for explaining the model's behavior across the whole dataset (global interpretability). Figure 1 shows how each method is used.

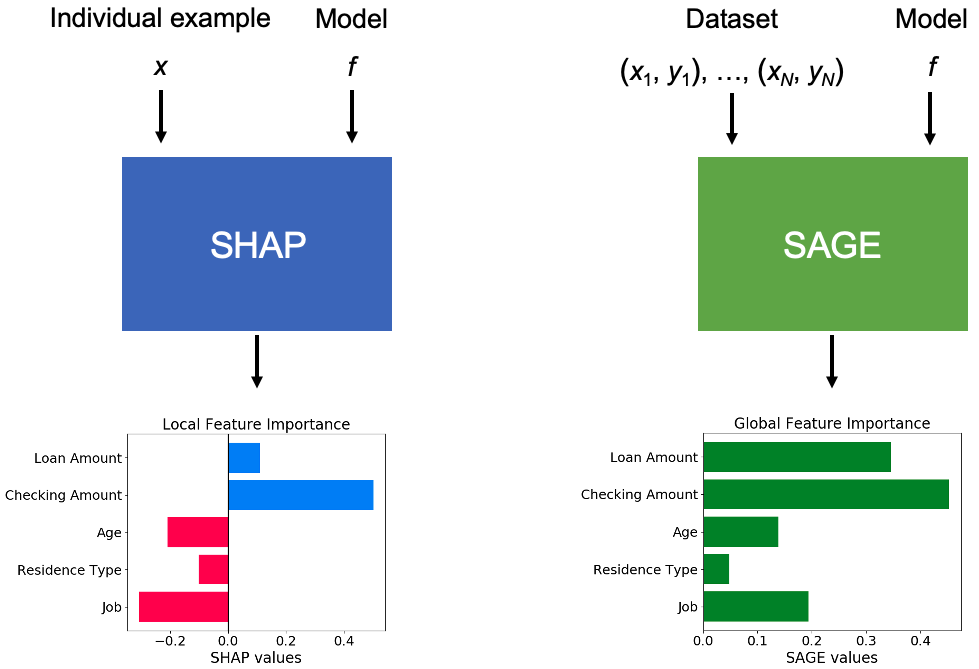
There are many approaches for both local and global interpretability, but SHAP and SAGE are particularly appealing because they answer their respective questions in a mathematically principled fashion, thanks to the Shapley value. This post explains their foundation in cooperative game theory, because this aspect of the methods is new to many users.

We'll start by reviewing the Shapley value, a concept from game theory that's essential for understanding SHAP and SAGE. We'll then see how SHAP and SAGE use Shapley values for model understanding, and finally we'll discuss how the two methods are connected.

Shapley values

Shapley values were developed by Lloyd Shapley in a 1953 paper [3] about assigning credit to players in a cooperative game. The paper was written in the field of game theory, so Shapley values actually have nothing to do with ML. We can illustrate the idea behind Shapley values using a scenario with no ML involved.

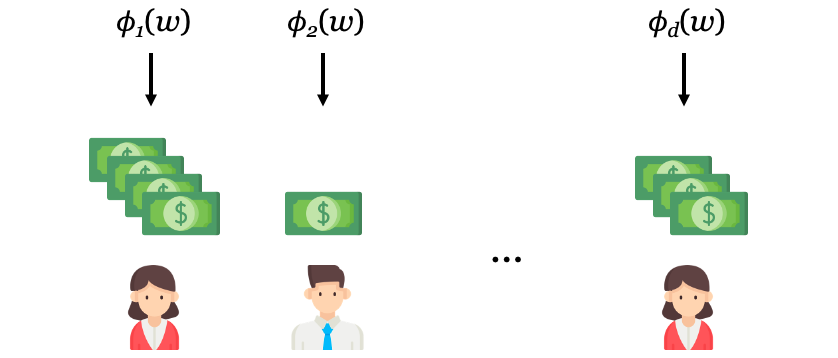
Imagine a company with $d$ employees who are represented by the set $D = \{1, 2, \ldots, d\}$. The company makes $1,000,000 a year in profits when all the employees do their job, and management wants to distribute the profits through bonuses (Figure 2). However, management wants to do so in a fair way, rewarding people in accordance with their contribution to the company's profits.

Management at this company is very insightful, so they have a powerful tool for quantifying each employee's contribution: they know exactly how profitable the company would have been with any subset $S \subseteq D$ of the employees doing their job. (People with normal jobs will point out that no real company has this information, but bear with me.) As a couple examples:

• With all the employees working ($S = D$) they make $1,000,000.
• If everyone stayed but they lost their CEO ($S = \{2, 3, \ldots, d\}$), they would make half as much money, $500,000.
• If they kept everyone except for a couple of new hires ($S = \{1, 2, \ldots, d - 2\}$), they would make almost as much profit, $950,000.
• If no one worked there ($S = \{\}$) they would make precisely zero dollars.

These are just a couple examples, but the management team knows exactly how profitable the company would be with all $2^d$ subsets of employees. Management then summarizes their knowledge with a profitability function

where $\mathcal{P}(D)$ represents the power set of $D$ (i.e., all subsets of $D$). For any subset of employees $S \subseteq D$, the quantity $w(S)$ is the amount of profit the company makes with the employees in $S$ working.

Armed with this knowledge, the management team holds a meeting to discuss giving bonuses $\phi_1(w), \phi_2(w), \ldots, \phi_d(w)$ to each employee $1, 2, \ldots, d$. (Note that the bonuses $\phi_i(w)$ depend on the profitability function $w$, because if $w$ were different then the bonuses should change.) When the team discusses what it means to allocate bonuses fairly, they come up with the following goals:

1. (Efficiency) The bonuses should add up to the difference between the profitability with all employees and the profitability with no employees, or $\sum_{i \in D} \phi_i(w) = w(D) - w(\{\})$.
2. (Symmetry) If two employees $i, j$ are interchangeable, so that their inclusion always yields the same result, with $w(S \cup \{i\}) = w(S \cup \{j\})$ for all $S$, then their bonuses should be identical, or $\phi_i(w) = \phi_j(w)$.
3. (Dummy) If employee $i$ contributes nothing, so that their inclusion yields no change in profitability, with $w(S \cup \{i\}) = w(S)$ for all $S$, then they should receive no bonus, or $\phi_i(w) = 0$.
4. (Linearity) If the company's total profitability function $w$ is viewed as the linear combination of separate profitability functions $w_1, w_2, \ldots, w_k$ for each of the company's $k$ businesses, or $w = c_1w_1 + c_2w_2 \ldots + c_kw_k$, then the bonus for each employee determined on the company level $\phi_i(w)$ should equal the linear combination of the employee's bonuses determined on the level of individual businesses $\phi_i(w_j)$, so that

These properties seem reasonable, so the management team wants the bonuses $\phi_i(w)$ to satisfy properties 1-4. The challenge is, it isn't immediately clear how to do this or if it's even possible.

It turns out that there is a way, and the fair bonus for each employee $i \in D$ is given by the following formula:

That formula looks complicated, but to calculate the bonus for employee $i$ we're basically considering the profitability increase from adding $i$ to a subset $S$, which is represented by

and then taking a weighted average of this quantity across all possible subsets $S$ that don't include $i$ already, or $S \subseteq D \setminus \{i\}$. The weights are a bit complicated, but this exact weighting scheme yields bonuses that satisfy properties 1-4. (If you're interested in understanding the weighting scheme, it comes from enumerating all possible orderings of the $d$ employees, and then averaging the profitability bump from adding employee $i$ across all those orderings.)

You may wonder where this formula comes from and how we know that it satisfies the properties listed above. The formula was the subject of Lloyd Shapley's famous paper from 1953 [1], where he showed that for any profitability function $w$ (cooperative game in game theory), the values $\phi_i(w)$ (the Shapley values of $w$) provide the unique way of assigning scores to each employee (player in game theory) that satisfy properties 1-4. He actually used a different set of properties, but subsequent work showed that there are multiple sets of properties (or axioms) that lead to the same result.

The formula for $\phi_i(w)$ given above is the Shapley value—it's a function of a set function $w$, and it provides a summary of the contribution of each player $i \in D$ to the total profit $w(D)$. Thanks to Lloyd Shapley, the management team can allocate bonuses using the Shapley value and know that they've been fair to their employees (Figure 3).

Hopefully this example has given you some intuition for Shapley values. We used the example of a company here, but Shapley values can be used to summarize contributions to any cooperative game $w: \mathcal{P}(D) \mapsto \mathbb{R}$. Next, we'll discuss how SHAP and SAGE use Shapley values to help understand ML models.

SHAP (SHapley Additive exPlanations)

Let's re-enter the world of ML and see how SHAP uses Shapley values to explain individual predictions.

Consider a ML model $f$ that predicts a response variable $y$ given an input $x$, where $x$ consists of individual features $(x^1, x^2, \ldots, x^d)$. We'll use uppercase symbols (e.g., $X$) to refer to random variables and lowercase symbols (e.g., $x$) to refer to values. SHAP is designed to explain why the model $f$ makes the prediction $f(x)$ given the input $x$.

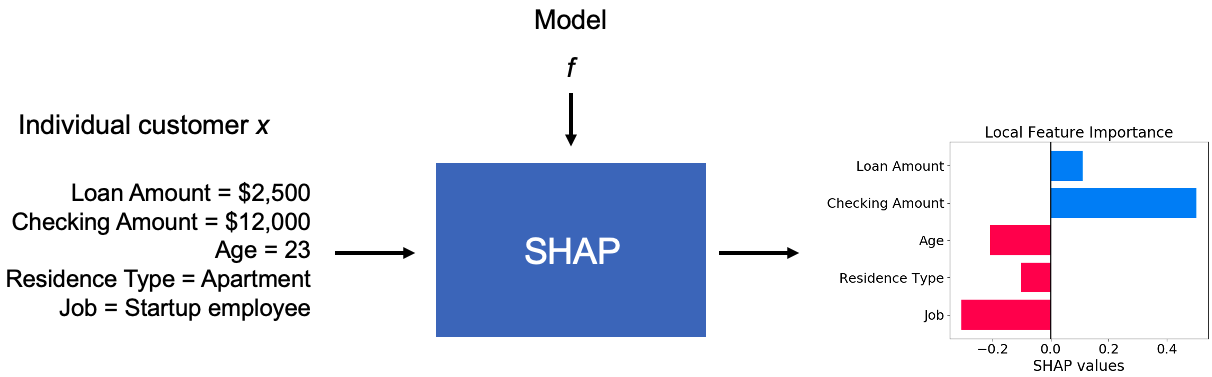
As a running example, let's consider a model used by a bank to assess the likelihood of loan repayment. To keep it simple let's say there are just five features: the loan amount, the amount in the customer's checking account, the customer's age, their residence type, and their job. The model $f$ predicts the probability that the loan will be repaid.

Let's also focus on a single customer. John is requesting a loan for $2,500, he has $12,000 in his checking account, he's a 23 year old startup employee, and he lives in an apartment. The model predicts $f(x) = 0.7$, or that there's only a 70% chance John will repay his loan. That's a bit low, and John wants to know if it's because of his age, his job, or something else.

SHAP explains an individual prediction by assigning values $\phi_1, \phi_2, \ldots, \phi_d$ to each feature $x^1, x^2, \ldots, x^d$ that quantify the feature's influence on the prediction $f(x)$ (Figure 4). More specifically, each feature's value represents a contribution to the amount by which $f(x)$ deviates from the mean prediction $\mathbb{E}[f(X)]$. In the case of the loan assessment model, we can use SHAP to understand why John's probability of repayment $f(x)$ seems lower (riskier) than the average customer's outcome $\mathbb{E}[f(X)]$.

To illustrate how SHAP works in an intuitive way, we'll imagine that our model is a human—an expert who is very good at making accurate predictions but not so good at explaining their logic. Furthermore, we'll assume that the expert is willing to make predictions given any subset of features (without knowing a customer's age, for example).

When the expert says that John seems risky, we might ask, "what if I hadn't told you that John works for a startup?" Perhaps the expert would say that John would seem more likely to repay. Or, we might ask, "what if I hadn't told you John's job, the fact that he's 23, or that he lives in an apartment?" Now the expert may say that John would seem much more likely to repay. By providing the expert with subsets of features, we can see whether holding out information moves the prediction higher or lower. This is a first step towards understanding the expert's logic.

It's a bit tougher to replicate this with a ML model $f$. Models are brittle and usually require a fixed set of features, so we can't just remove features and ask for a prediction given $x^S$ for some $S \subseteq D$. SHAP therefore proposes a way of letting the model accommodate missing features.

SHAP defines the cooperative game $v_{f, x}$ to represent a prediction given the features $x^S$, as

That means that the values $x^S$ are known, but the remaining features are treated as a random variable $X^{\bar S}$ (where $\bar S = D \setminus S$), and we take the mean prediction $f(X)$ when the unknown values follow the conditional distribution $X^{\bar S} \; | \; X^S = x^S$.

Given this convention for making predictions using subsets of features, we can apply the Shapley value to define each feature's contribution to the prediction $f(x)$ using the Shapley values $\phi_i(v_{f, x})$. This is just like what we did with the imaginary company, except we're replacing employees with features and the company's profitability with the model's prediction. The features containing the most evidence for successful repayment will have large positive values $\phi_i(v_{f,x}) > 0$, while uninformative features will have small values $\phi_i(v_{f, x}) \approx 0$, and features containing evidence for a failure to repay will have negative values $\phi_i(v_{f, x}) < 0$. These Shapley values are known as SHAP values.

That's SHAP in a nutshell. There's more to it in practice because calculating $\phi_i(v_{f, x})$ is computationally challenging: in fact, one of the SHAP paper's biggest contributions was proposing fast approximations that improve on the algorithm from the IME paper a couple years earlier [1, 4]. We won't talk about approximation in detail here, but KernelSHAP is fast and model-agnostic [1] and TreeSHAP is even faster because it's specific to tree-based models [5].

SAGE (Shapley Additive Global importancE)

Now we'll see how SAGE applies Shapley values to provide a different kind of model understanding: this time we want to explain how much $f$ relies on each feature $X^1, X^2, \ldots, X^d$ overall (Figure 5).

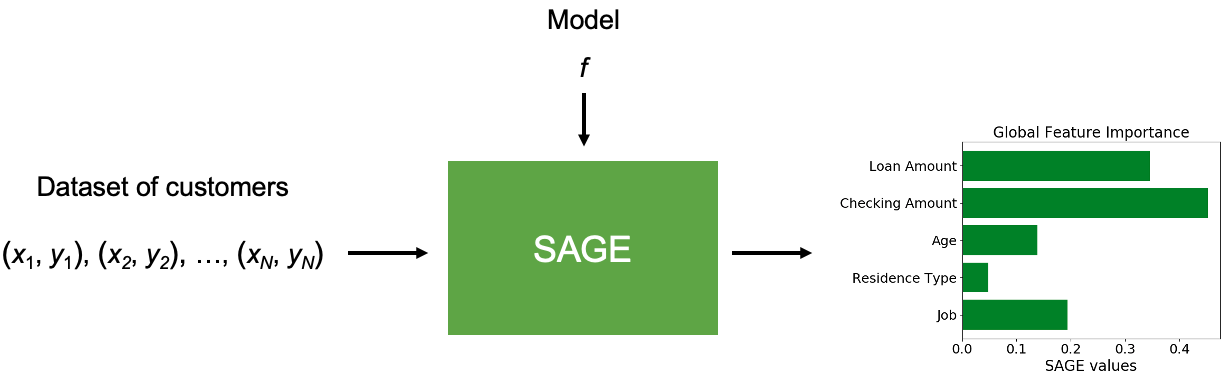
How do we figure out which features are most important to a model? To get some intuition for SAGE, let's go back to the human expert who makes good predictions but can't explain their logic.

To understand which features the expert derives the most information from, we can run an experiment where we deprive them of information and see how much their prediction accuracy suffers. For example, we can take a large sample of customers and ask the expert to predict their probability of repayment given everything but the customer's age. Their accuracy will probably drop by a little bit. Or, we can ask the expert to predict the probability of repayment given everything except age, checking account balance and job. Now their accuracy should drop by a lot because they're being deprived of critical information.

To apply the same logic to a ML model $f$, we must once again confront the problem that $f$ requires a fixed set of features. We can use the same trick as above and deal with missing features using their conditional distribution $X^{\bar S} \; | \; X^S = x^S$. We can now define a cooperative game that represents the model's performance given subsets of features. Given a loss function $\ell$ (e.g., MSE or cross entropy loss), the game $v_f$ is defined as

For any subset $S \subseteq D$, the quantity $v_f(S)$ represents $f$'s performance given the features $X^S$, and we have a minus sign in front of the loss so that lower loss (improved accuracy) increases the value $v_f(S)$.

Now, we can use the Shapley values $\phi_i(v_f)$ to quantify each feature's contribution to the model's performance. The features that are most critical for the model to make good predictions will have large values $\phi_i(v_f) > 0$, while unimportant features will have small values $\phi_i(v_f) \approx 0$, and only features that make the model's performance worse will have negative values $\phi_i(v_f) < 0$. These are SAGE values, and that's SAGE in a nutshell.

The paper describes SAGE and its properties in more detail, and it also proposes an algorithm for estimating SAGE values efficiently [2]. On the theory side, the paper shows that SAGE provides insight about intrinsic properties of the data distribution (which might be called explaining the data, rather than explaining the model) and that SAGE unifies a number of existing feature importance methods. We touch on both points briefly below.

Explaining the data. SAGE is primarily a tool for model interpretation, but it can also be used to gain insight about intrinsic relationships in the data. For example, when SAGE is applied with the Bayes classifier $f(x) = p(y \; | \; x)$ and cross entropy loss, SAGE values are equal to the Shapley values of the mutual information function $v_f(S) = I(Y; X^S)$. This is good news for users who use ML to learn about the world (e.g., which genes are associated with breast cancer) and who aren't as interested in models for their own sake.

Unifying global feature importance methods. The paper proposes a class of methods that provide additive approximations of the predictive power contained in subsets of features. The framework of additive importance measures connects a number of methods that were previously viewed as unrelated. For example, we can see how SAGE differs from permutation tests, one of the methods in the framework.

Permutation tests, proposed by Leo Breiman for assessing feature importance in random forest models, calculate how much the model performance drops when each column of the dataset is permuted [6]. SAGE can be viewed as modified version of a permutation test:

• Instead of holding out one feature at a time, SAGE holds out larger subsets of features. (By only removing individual features, permutation tests may erroneously assign low importance to features with good proxies.)
• SAGE draws held out features from their conditional distribution $p(X^{\bar S} \; | \; X^S = x^S)$ rather than their marginal distribution $p(X^{\bar S})$. (Using the conditional distribution simulates a feature's absence, whereas using the marginal breaks feature dependencies and produces unlikely feature combinations.)

This is SAGE in a nutshell, and hopefully this helps you understand its foundation in game theory.

How SHAP and SAGE are related

SHAP and SAGE both use Shapley values, but since they answer fundamentally different questions about a model (local versus global interpretability), it isn't immediately clear whether their connection goes deeper.

It turns out that there is no simple relationship between SAGE values $\phi_i(v_f)$ and SHAP values $\phi_i(v_{f, x})$. However, SAGE values are related to a SHAP variant known as LossSHAP [5]. Instead of explaining an individual prediction using the cooperative game $v_{f, x}$, we can use a game $v_{f, x, y}$ that represents the loss for an individual input-output pair $(x, y)$ given subsets of features $x^S$:

The Shapley values of this game $\phi_i(v_{f, x, y})$ are called LossSHAP values, and they represent how much each feature contributes to the prediction's accuracy. Features that make the prediction more accurate have large values $\phi_i(v_{f, x, y}) > 0$, and features that make the prediction less accurate have negative values $\phi_i(v_{f, x, y}) < 0$.

The SAGE paper shows that SAGE values are equal to the expectation of the LossSHAP values [2]. Mathematically, we have

The connection is important because it shows that a global explanation can be obtained via many local explanations: SAGE values can be calculated by calculating LossSHAP values for the whole dataset and then taking the mean, as illustrated in Figure 6.

However, waiting for LossSHAP values to converge for hundreds or thousands of examples in the dataset is very slow. The SAGE paper therefore proposes a faster approximation algorithm that aims directly at a global explanation—an approach we'll refer to as SAGE sampling. With SAGE sampling, SAGE values can be calculated in the same amount of time as just a handful of individual LossSHAP values. Figure 7 shows a comparison of the convergence of LossSHAP values and SAGE values for a gradient boosting machine trained on the German Credit dataset, where a global explanation is calculated at the cost of just ${\approx}10$ local explanations.

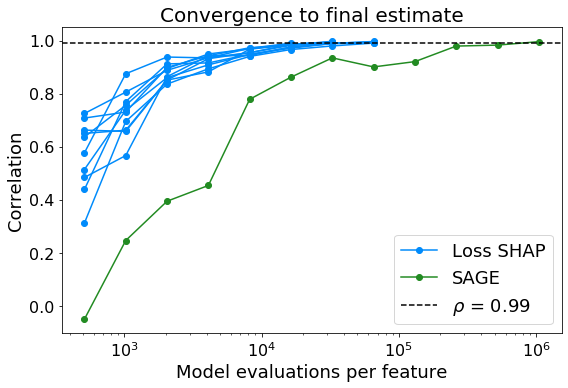
Table 1 provides a comparison of SHAP, LossSHAP and SAGE values. Each method is built on Shapley values, but they answer different questions about ML models.

Table 1: Comparison of SHAP, LossSHAP and SAGE values.

	SHAP	LossSHAP	SAGE
Type of explanation	Local	Local	Global
Cooperative game	$v_{f, x}$	$v_{f, x, y}$	$v_f$
Feature values	$\phi_i(v_{f, x})$	$\phi_i(v_{f, x, y})$	$\phi_i(v_f)$
Meaning	Contribution to prediction $f(x)$	Contribution to accuracy of $f(x)$	Contribution to $f$'s performance
Approximation	IME [4] KernelSHAP [1] TreeSHAP [5]	LossSHAP sampling [2] TreeSHAP [5]	Mean LossSHAP value [2] SAGE sampling [2]

Conclusion

Hopefully this post has given you a better understanding of Shapley values, as well as SHAP, SAGE and LossSHAP. Shapley values are pretty easy to understand outside the ML context (like with our example of a company that wants to give fair bonuses), and it's natural to apply the same logic to ML models once we deal with the fact that models require fixed sets of features.

These methods are easy to use, so you should check them out: SHAP's Github page is here and SAGE's Github page is here.

Summary of notation:

• $w(S)$: the company's profitability function given the employee subset $S$.
• $v_{f, x}(S)$: the model $f$'s prediction given the features $x^S$ (for SHAP values).
• $v_f(S)$: the model $f$'s performance (negative loss) given the features $X^S$ (for SAGE values).
• $v_{f, x, y}(S)$: the negative loss of $f$'s prediction given $x^S$ and label $y$ (for LossSHAP values).

References

1. Scott Lundberg, Su-In Lee. "A Unified Approach to Interpreting Model Predictions." Neural Information Processing Systems, 2017.
2. Ian Covert, Scott Lundberg, Su-In Lee. "Understanding Global Feature Contributions With Additive Importance Measures." Neural Information Processing Systems, 2020.
3. Lloyd Shapley. "A Value for n-Person Games." Contributions to the Theory of Games, 1953.
4. Erik Strumbelj, Igor Kononenko. "An Efficient Explanation of Individual Classifications Using Game Theory." Journal of Machine Learning Research, 2010.
5. Scott Lundberg et al. "From Local Explanations to Global Understanding with Explainable AI for Trees." Nature Machine Intelligence, 2020.
6. Leo Breiman. "Random Forests." Machine Learning, 2001.

Acknowledgements

All the icons used in my diagrams were made by Freepik and are available at www.flaticon.com.