Choosing the right temperature for the Concrete distribution

By Ian Covert June 2, 2020

The Concrete distribution is a really powerful tool for modern machine learning. We use it to learn the parameters of discrete distributions, but it's actually a continuous distribution on the probability simplex. The temperature parameter controls the sparsity of samples, and although I've been using the Concrete distribution for a while, I've never been certain that I'm using the right temperature value.

So that's what I've tried to figure out for this post. I'll start by explaining the role of the temperature parameter through the Concrete's relationship with other random variables (namely, the Gumbel and Generalized Inverse Gamma), and then I'll run some simulations that provide practical guidance on how to set it in your models.

Introduction to the Concrete distribution

Before saying what the Concrete distribution is, here's why it's so famous. Starting in 2013, a technique known as the reparameterization trick (explained here) became popular for learning distributions of random variables inside neural networks [1, 2]. Learning distributional parameters can be tricky, but these papers showed how to get an unbiased, low-variance gradient estimator using a clever sampling trick. There were other techniques before it, but the reparameterization trick's low variance made it work much better, especially for VAEs. But unfortunately, although it worked for a variety of distributions (Gaussian, Gamma, Weibull, etc.), it didn't work out-of-the-box for discrete random variables.

Then, the Concrete distribution showed how to make it work. The distribution, introduced by two papers in 2016, is a continuous relaxation for discrete random variables (hence the name con-crete) [3, 4]. When you think about discrete random variables, you probably think of a random variable with the possible values $\{1, 2, \ldots, n\}$ , but that set is equivalent to the set of $n$ one-hot vectors in $\mathbb{R}^n$ . And the Concrete distribution is basically a relaxed version of a distribution over one-hot vectors. Its support is on the $n-1$ simplex

$\Delta^{n-1} = \{x \in [0, 1]^n: \sum_{i=1}^n x_i = 1\},$

whereas one-hot vectors lie at the vertices

$\mathrm{Vert}(\Delta^{n-1}) = \{x \in \{0, 1\}^n: \sum_{i=1}^n x_i = 1\}.$

The Concrete distribution over $n$ indices has $n + 1$ parameters. There are $n$ unnormalized probabilities $\alpha_1, \ldots, \alpha_n \geq 0$ that control how likely each index is to dominate the others, and there's a temperature parameter $\lambda > 0$ that controls the sparsity of samples.

Formally, the distribution is defined by its density function $p_{\alpha, \lambda}(x)$ , which for $X \sim \mathrm{Concrete}(\alpha, \lambda)$ can be written as

$p_{\alpha, \lambda}(x) = (n-1)! \lambda^{n-1} \prod_{i=1}^n \frac{\alpha_i x_i^{-\lambda - 1}}{\sum_{k=1}^n \alpha_k x_k^{-\lambda}}$

for $x \in \Delta^{n-1}$ [3]. That may not seem very intuitive, but we'll see a couple simpler ways to understand the Concrete distribution below.

First, here's what the samples look like for different sets of parameters.

Figure 1: Samples of $X \sim \mathrm{Concrete}(\alpha, \lambda)$ for different values of $\lambda$ , with $n = 10$ and $\alpha_i = \frac{1}{10}$ .

As you can see, the samples get more discrete/sparse as the temperature $\lambda$ is set to lower values. And since we usually want discrete samples, the ability to set the temperature is an essential feature of the Concrete distribution.

To see why the temperature has this effect, we need to consider how the Concrete relates to other random variables.

In terms of independent uniform samples $U_i \sim \mathrm{Uniform}(0, 1)$ , the random variable $X \sim \mathrm{Concrete}(\alpha, \lambda)$ has dimensions $X_1, \ldots, X_n$ equal to
$X_i = \frac{e^{(\log \alpha_i - \log (- \log U_i))/\lambda}}{\sum_{k=1}^n e^{(\log \alpha_k - \log (- \log U_k))/\lambda}}$
This is how we typically sample from the Concrete distribution in practice. But the expression above isn't very intuitive.
In terms of independent Gumbel samples $G_i \sim \mathrm{Gumbel}(0, 1)$ , the random variable $X \sim \mathrm{Concrete}(\alpha, \lambda)$ has dimensions $X_1, \ldots, X_n$ equal to
$X_i = \frac{e^{(\log \alpha_i + G_i)/\lambda}}{\sum_{k=1}^n e^{(\log \alpha_k + G_k) / \lambda}}$
or $X = \mathrm{softmax}(\frac{\log \alpha_1 + G_1}{\lambda}, \ldots, \frac{\log \alpha_n + G_n}{\lambda})$ . This is what gives the Concrete distribution its other name, the Gumbel-softmax distribution [4]. And you can see that a low temperature $\lambda$ would amplify the differences between the softmax arguments and lead to a one-hot vector.
An interpretation that I find even simpler is that $X \sim \mathrm{Concrete}(\alpha, \lambda)$ has dimensions $X_1, \ldots, X_n$ equal to
$X_i = \frac{V_i}{\sum_{k=1}^n V_k}$
where $V_i \sim \mathrm{GenInvGamma}(\alpha_i^{-1/\lambda}, \lambda, \lambda)$ . So each dimension of the Concrete represents the proportion of the sum of $n$ independent Generalized Inverse Gamma random variables.

That last part about the Generalized Inverse Gamma variables makes the Concrete look a bit like the Dirichlet distribution (another distribution on the probability simplex), because the random variable $Y \sim \mathrm{Dirichlet}(\beta)$ has dimensions $Y_1, \ldots, Y_n$ equal to

$Y_i = \frac{W_i}{\sum_{k=1}^n W_k}$

where $W_i \sim \mathrm{Gamma}(\beta_i, \theta)$ , or equivalently $W_i \sim \mathrm{GenGamma}(\theta, \beta_i, 1)$ . So the Concrete and Dirichlet distributions are actually pretty similar: they're both proportions of $n$ independent non-negative random variables, and both depend on the Gamma distribution. Table 1 provides a comparison between the Concrete and Dirichlet distributions, and it highlights how both can be understood in terms of other distributions.

Table 1: Concrete distribution versus Dirichlet distribution.
	Concrete	Dirichlet
Parameters	$\alpha_1, \alpha_2, \ldots, \alpha_n \geq 0$ $\lambda > 0$	$\beta_1, \beta_2, \ldots, \beta_n \geq 0$
Support	$\Delta^{n-1}$ for $\lambda > 0$ $\mathrm{Vert}(\Delta^{n-1})$ for $\lambda = 0$	$\Delta^{n-1}$
Proportion of	$V_i \sim \mathrm{GenInvGamma}(\alpha_i^{-1/\lambda}, \lambda, \lambda)$	$W_i \sim \mathrm{Gamma}(\beta_i, \theta)$
Softmax of	$P_i \sim \mathrm{Gumbel}(\frac{\log \alpha_i}{\lambda}, \frac{1}{\lambda})$	$Q_i \sim \mathrm{LogGamma}(\beta_i, \theta)$
Primary Uses	Learning discrete distributions	Conjugate prior Topic modeling

The Concrete and Dirichlet distributions have some similarities, but their differences are significant. The Gamma distribution used by the Dirichlet is well-behaved: $W_i$ has finite mean, and all of its moments exist. By contrast, the Generalized Inverse Gamma is heavy-tailed: for low temperatures $\lambda$ , the mean, variance, and higher moments of $V_i$ are all undefined [5]. Intuitively, that means that empirical estimators for these quantities would never converge because the occasional massive samples would throw them off. So at low temperatures $\lambda \approx 0$ , the Concrete distribution is much more likely to have individual samples $V_i$ that make up a large proportion of the total $\sum_{k=1}^n V_k$ , which leads to values of $X$ near $\mathrm{Vert}(\Delta^{n-1})$ .

This perspective gives some intuition for why low temperatures have the effect of increasing the sparsity of Concrete samples. If you're interested, check out the derivation of these results below.

Consider the sequence of operations that we use to produe a Concrete sample using the Gumbel-softmax trick. For convenience, we'll use $A, B, C\ldots$ to denote the sequence of random variables.

Given $A \sim \mathrm{Uniform}(0, 1)$ , $B = - \log A$ has distribution $B \sim \mathrm{Exponential}(1)$ .
$C = - \log B$ has distribution $C \sim \mathrm{Gumbel}(0, 1)$ .
$D = \log \alpha + C$ has distribution $D \sim \mathrm{Gumbel}(\log \alpha, 1)$ .
$E = e^{-D} = \frac{1}{\alpha}e^{- C} = \frac{1}{\alpha} B$ has distribution $E \sim \mathrm{Exponential}(\alpha)$ , or equivalently $E \sim \mathrm{Gamma}(1, \alpha^{-1})$ (using the shape-scale parameterization).
$F = E^{\frac{1}{\lambda}}$ has distribution $F \sim \mathrm{GenGamma}(\alpha^{-1/\lambda}, \lambda, \lambda)$ .
$G = \frac{1}{F}$ has distribution $G \sim \mathrm{GenInvGamma}(\alpha^{-1/\lambda}, \lambda, \lambda)$ .
A Concrete random variable $X \sim \mathrm{Concrete}(\alpha, \lambda)$ is therefore equal to $X_i = \frac{G_i}{\sum_{k=1}^n G_k}$
where $G_i \sim \mathrm{GenInvGamma}(\alpha_i^{-1/\lambda}, \lambda, \lambda)$ . And if you're wondering about the relationships between all these different probability distributions, here's where you can learn more about them: Exponential, Gumbel, Gamma, Generalized Gamma, Generalized Inverse Gamma, Dirichlet.

Now, let's talk about the tradeoff we face when choosing a temperature value. What happens when we choose a high temperature or a low temperature?

High temperature

In the limit $\lambda \rightarrow \infty$ , samples from the Concrete distribution aren't like one-hot vectors at all. In fact, they're deterministically equal to $(\frac{1}{n}, \ldots, \frac{1}{n})$ , with the mass spread evenly between the indices [4]. Formally, we would say that for $X_\lambda \sim \mathrm{Concrete}(\alpha, \lambda)$ we have

$\lim_{\lambda \rightarrow \infty} X_\lambda = (\frac{1}{n}, \ldots, \frac{1}{n}).$

This seems intuitive when you think about the Gumbel-softmax sampling trick, because a large temperature wipes out any differences between the arguments to the softmax.

Low temperature

In the limit $\lambda \rightarrow 0$ , the samples start to actually look like one-hot vectors. This was proved in Proposition 1c of [3], where the authors showed that

$P(\lim_{\lambda \rightarrow 0} X_i = 1) = \frac{\alpha_i}{\sum_{k=1}^n \alpha_k}.$

Again, the increasing sparsity of the samples seems obvious when you consider the role of the temperature in the softmax. The fact that the probability of $X_i$ dominating the other indices is equal to $\alpha_i / \sum_{k=1}^n \alpha_k$ is the magic of the Gumbel-max trick (which predates the Gumbel-softmax trick by several decades). Ryan Adams has a simple proof of this fact here.

An easy choice?

Given what we've just seen, this seems like an easy choice—we should just use $\lambda \approx 0$ to get more discrete samples, right? Unfortunately, there's a tradeoff: the original paper explains that low $\lambda$ is necessary for discrete samples, but high $\lambda$ is necessary for getting large gradients [3]. And we need large gradients to learn the parameters $(\alpha_1, \ldots, \alpha_n)$ .

Figure 2: The tradeoff with the temperature parameter $\lambda$ .

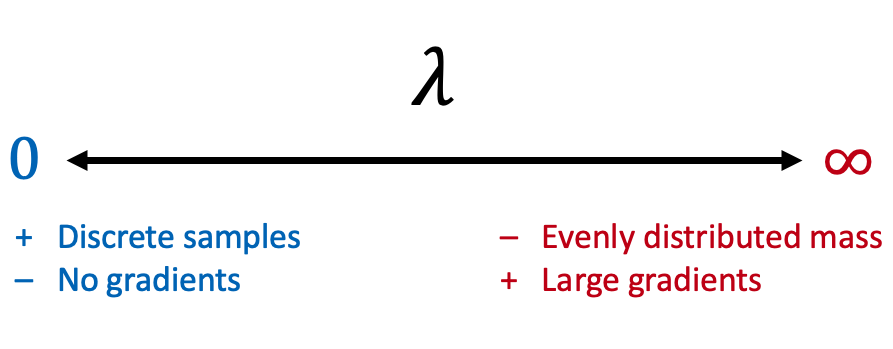
To deal with the tradeoff, some papers have used a carefully chosen fixed value of $\lambda$ [6], while others have annealed $\lambda$ from a high value to a low value [7]. I like the idea of annealing, because you can pass through a region of high $\lambda$ that's suitable for learning while eventually ending up with discrete samples. Learning will get harder as $\lambda$ gets closer to zero, but you should end up with a good solution for $\lambda$ if you pre-solve the problem for a slightly larger $\lambda'$ .

So annealing seems like a good idea, but to do it, we still need to figure out a range of values that makes sense.

Choosing the right temperature

What does it mean to choose the right temperature value? We want a large enough temperature to enable learning, but we also want a low enough temperature to get discrete samples. That's why annealing from a high value to a low value is a nice idea, because we can get the best of both worlds. We know how the Concrete distribution behaves when $\lambda \rightarrow \infty$ or $\lambda \rightarrow 0$ , and we want to pass between these two regimes when we anneal $\lambda$ . The question is where the transition occurs.

To figure this out, I tried to derive a mathematical function to describe the sparsity of Concrete samples as a function of $\alpha$ and $\lambda$ . Sadly, this turned out to be very hard. My plan was to quantify the sparsity of single samples though their entropy, or the value of the maximum index, and then figure out what that quantity was in expectation. It turns out that the inverse of the maximum index $M^{-1} = (\max_i X_i)^{-1}$ is a bit easier to characterize, but figuring out $\mathbb{E}[M^{-1}]$ was still too hairy. Maybe someone else will figure it out one day.

Until then, we can fall back on a simulation study. The idea is to consider different values of $n$ and $\lambda$ to see how the sparsity of Concrete samples changes. Of course we should also look at different values of $\alpha$ , but it seems obvious that letting $\alpha = (\frac{1}{n}, \ldots, \frac{1}{n})$ will lead to the most spread out samples, so we'll just look at this "balanced" setting, plus one "imbalanced" setting where $\alpha_1 = 0.9$ and the rest are $\alpha_2 = \ldots = \alpha_n = \frac{0.1}{n - 1}$ .

We'll use two quantities to measure sparsity. First, we'll look at the average entropy of samples, $\mathbb{E}[H(x)]$ , by which I mean the entropy in the discrete random variable $Y \sim \mathrm{Categorical}(x)$ . And second, we'll look at the expected value of the max index, $\mathbb{E}[M] = \mathbb{E}[\max_i X_i]$ .

I estimated each of these quantities for 100 different temperature values using a million samples, and the results demonstrate exactly what we want to see. The transition between perfect spread and perfect sparsity happens between $\lambda = 10.0$ and $\lambda = 0.01$ for a wide range of numbers of indices $n \in \{10, 100, 1{,}000, 10{,}000\}$ .

Figure 3 shows that the mean entropy starts out high and then goes to zero, and we start getting sparse samples without having to resort to extremely low temperatures. Even for large values of $n$ and balanced parameters, the samples have almost no entropy with $\lambda = 0.1$ . And when the parameters are imbalanced, we can get sparse samples with even higher temperatures.

Figure 3: The mean entropy of samples from the Concrete distribution for different values of $n, \lambda$ , with two settings of $\alpha$ . Horizontal lines show the maximum possible entropy for each value of $n$ .

Figure 4 shows the expected value of the max index $\mathbb{E}[\max_i X_i]$ , and these simulations tell the same story. According to these results, it would be safer to set the temperature to $\lambda = 0.01$ to get truly discrete samples when $\alpha$ is balanced, but for imbalanced parameters we can get near exact sparsity with $\lambda = 0.1$ .

Figure 4: The mean max value of samples from the Concrete distribution for different values of $n, \lambda$ , with two settings of $\alpha$ . Horizontal lines show the minimum possible max value for each value of $n$ .

These results show that if you want to start with a high temperature to make learning easier, then there's no point in going higher than $\lambda = 10.0$ . And if you want to reduce the temperature to get truly discrete samples, then $\lambda = 0.01$ should be sufficient. Even for reasonably large values of $n$ , annealing the temperature between $\lambda = 10.0$ and $\lambda = 0.01$ allows you to transition between the two regimes, so you can get the best of both worlds by taking advantage of larger gradients for learning while still ending up with discrete samples.

Conclusion

The Concrete distribution is a powerful tool because it lets us learn the parameters of discrete distributions with the reparameterization trick, but the low temperatures that are necessary for truly discrete samples can make learning harder. These simulations gave us a good idea of the right range of $\lambda$ values to use during training by showing where the transition occurs between perfect spread and perfect sparsity.

According to the results in these simulations, multiplicatively annealing the temperature from $\lambda = 10.0$ to $\lambda = 0.01$ (as in the Concrete Autoencoders paper [7]) or even just setting $\lambda = 0.1$ (the fixed value used by L2X [6]) should be effective both for learning, and for ultimately getting discrete samples. That's what I'll be doing from now on.

References

Diederik Kingma, Max Welling. "Auto-encoding Variational Bayes." International Conference on Learning Representations, 2013.
Danilo Rezende, Shakir Mohamed, Daan Wierstra. "Stochastic Backpropagation and Approximate Inference in Deep Generative Models." International Conference on Machine Learning, 2014.
Chris Maddison, Andriy Mnih, Yee Whye Teh. "The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables." International Conference on Learning Representations, 2016.
Eric Jang, Shixiang Gu, Ben Poole. "Categorical Reparameterization with Gumbel-Softmax." International Conference on Learning Representations, 2016.
Leigh Halliwell. "Classifying the Tails of Loss Distributions." Casualty Actuarial Society E-Forum, Spring 2013.
Jianbo Chen et al. "Learning to Explain: An Information-Theoretic Perspective on Model Interpretation." International Conference on Machine Learning, 2018.
Abubakar Abid, Muhammad Fatih Balin, James Zou. "Concrete Autoencoders for Differentiable Feature Selection and Reconstruction." International Conference on Machine Learning, 2019.

Choosing the right temperature for the Concrete distribution

Introduction to the Concrete distribution

Derivation

Choosing the right temperature

Conclusion

References